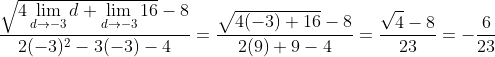Properties of Limits
When computing the value of a limit, it's possible to find one of these situations:
- The result is an expression that always has the same value. The most trivial case is when it's a real number like 5, 5/2, 0, etc.
-
Other expressions are less obvious but they are also known as determinate forms.
Some of them are shown below along with their results:
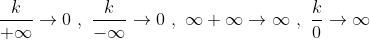
-
The result is an expression which value can change from one limit to another. These
are called Indeterminate and they don't have any fixed value. Some of them are shown below
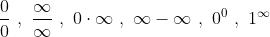
If a limit exists, the following properties of limits give us the necessary tools to compute it. Below we assume these limits exist:

Sum / Subtraction Rule
This rule states that the limit of the sum or subtraction of two functions is equal to the sum or subtraction of their limits:
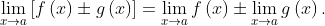
Constant Function Rule
The limit of a constant function is the constant:
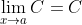
Constant Multiple Rule
The limit of a constant times a function is equal to the product of the constant and the limit of the function:
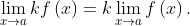
Product Rule
The limit of the product of two functions is the product of their limits
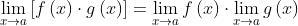
Quotient Rule
The limit of quotient of two functions is the quotient of their limits, provided that the limit in the denominator function is not zero:
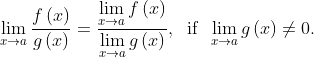
Power Rule
The limit of the power of a function to a given exponent n is the power n of the limit, where n is any real number
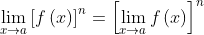
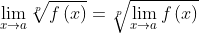
Example
Find the following limit:
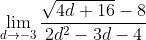
Appliyng the quotient rule:

Appliyng the sum / subtraction rule:
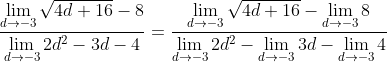
The next step requires the application of the power rule (for radicals), constant Multiple rule, and the constant function rule:
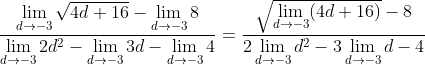
Operating into the radical and substituting in the explicit functions:
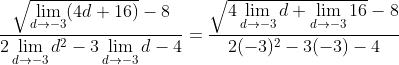
Operating the rest of the limits and simplifying: