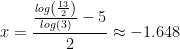Exponential Functions
An exponential growth or decay function is a function that grows or shrinks at a constant percent rate. The equation can be written in the form
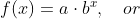
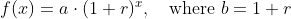
Where:
a is the initial or starting value of the function
r is the percent growth or decay rate, written as a decimal
b is the growth factor or growth multiplier.
Since powers of negative numbers behave strangely, we limit b to positive values
Finding the value of quantities with an exponential behavior
Let's explain this with an example:
A population of 1000 is decreasing 4% each year. Find the population in 25 years.
The initial value of the function is a=1000. Since we know the population is decreasing, the value of r is negative, i.e. r = -4/100 = -0.04. We now apply the equation for x = 25:

Finding Equations of Exponential Functions
In the previous example, we were able to find the value for the exponential function since we knew the initial quantity and the growth/decay rate. If we do not know any of them, but instead know only some input and output pairs of values, we can still construct the exponential function by managing the properties of the exponentials.
Example: In 2008, 85 deer were reintroduced into a wildlife refuge area from which the population had previously been hunted to elimination. By 2016, the population had grown to 191 deer. If this population grows exponentially, find a formula for the function. Find the estimated population in 2019.By defining our input variable to be t, years after 2008, the information listed can be written as two input-output pairs: (0,85) and (8,191).
Notice that by choosing our input variable to be measured as years after the first year value provided, we have effectively provided the initial value for the function: a = 85. This gives us an equation of the form
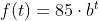
Substituting in our second input-output pair allows us to solve for b:
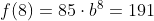
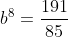
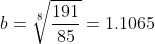
This gives us our equation for the population:
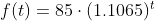
Recall that since b = 1+r, we can interpret this to mean that the population growth rate is r = 1.1065 - 1 = 0.1065, and so the population is growing by about 10.65% each year.
In the following example we cannot provide any of the values of the equation.
Example: Find a formula for an exponential function passing through the points (-2,6) and (2,1)
Since we don’t have the initial value, we will take a general approach that will work for
any function form with unknown parameters. We will substitute in both given input-output
pairs in the function form 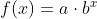 and solve for the unknown values, a and b.
and solve for the unknown values, a and b.
Substituting in (-2, 6) gives 
Substituting in (2, 1) gives 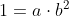
Solving  for a:
for a: 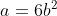
Substituting into the second equation

Operating
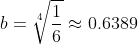
Going back to the equation 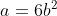
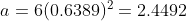
Putting this together gives the equation

The Logarithmic Function
Definition
A population of 50 flies is expected to double every week, leading to a function of the
form 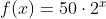 where x represents the number of weeks that have passed.
When will this population reach 500? Trying to solve this problem leads to the equation:
where x represents the number of weeks that have passed.
When will this population reach 500? Trying to solve this problem leads to the equation:
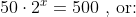
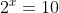
We know that 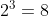 and
and
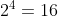 , so it is clear that x must be some value between 3 and 4 being
f(x) continuous and increasing. None of the functions we have already discussed would serve as
an inverse function and so we must introduce a new function, named log as the inverse of an
exponential function. Since exponential functions have different bases, we will define corresponding
logarithms of different bases as well.
, so it is clear that x must be some value between 3 and 4 being
f(x) continuous and increasing. None of the functions we have already discussed would serve as
an inverse function and so we must introduce a new function, named log as the inverse of an
exponential function. Since exponential functions have different bases, we will define corresponding
logarithms of different bases as well.
Logarithm
The logarithm (base b) function, written
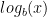 , is the inverse of the
exponential function (base b), thus it follows that:
, is the inverse of the
exponential function (base b), thus it follows that:
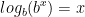
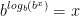
Logarithm Equivalent to an Exponential
The statement
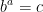 is equivalent to the statement
is equivalent to the statement
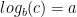
Examples. Rewrite these exponential equations as logarithmic equations:
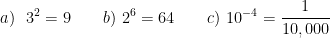
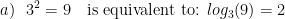
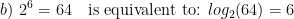

Examples. Rewrite these logarithmic equations as exponential equations:
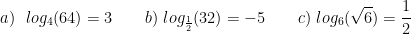
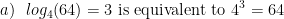
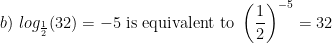
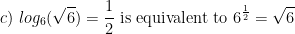
Common and Natural Logarithms
The common log is the logarithm with base 10, and is typically written log(x)
The natural log is the logarithm with base e, and is typically written ln(x), where e=2.71828182
Evaluating expressions whith logarithms means we must find an exponential relationship between the base and the argument of the function, so it can be expressed as a rational number. Recall the definition:
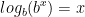
Examples:
Evaluate the following expressions:
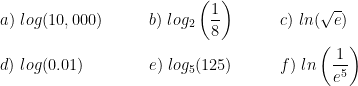
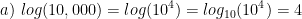
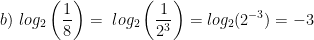
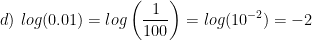
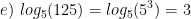
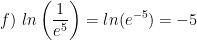
Properties of Logs: Change of Base:
Since our calculators and computers can usually evaluate the natural log or the common log, we might need to use a formula to change the base of a log to a known base. The formula is introduced below.
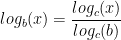
Example: Compute: 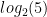
We apply the change of base formula:
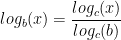
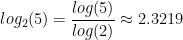
Properties of Logs: Exponent Property:
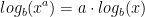
Examples:
Rewrite the following expressions using the exponent property of logarithms:
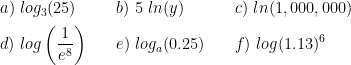
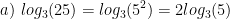
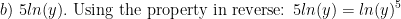
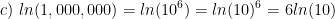
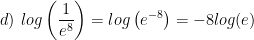
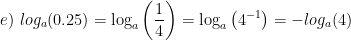
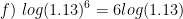
Solving exponential equations:
We'll follow the below procedure:
- Isolate the exponential expressions when possible
- Take the logarithm of both sides
- Utilize the exponent property for logarithms to pull the variable out of the exponent
- Use algebra to solve for the variable
Example: Solve for x: 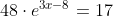
Isolate the exponential expression:

Take the logarithm of both sides:
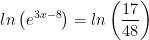
Utilize the exponent property for logarithms:
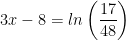
Use algebra to solve for x:
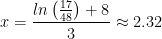
Example: Solve for x: 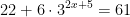
Isolate the exponential expression:
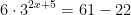
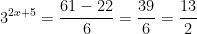
Take the logarithm of both sides:
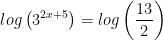
Utilize the exponent property for logarithms:
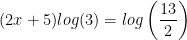
Use algebra to solve for x: