Cauchy and Heine Definitions of Limit
The limit of a function describes the value that the function approaches as the input approaches a particular point. Formally, if f(x) is a function and c is a point in its domain the limit of f(x) as the x approaches c is denoted as:
limx→cf(x)=L
where L is the value that f(x) gets closer to as the x gets closer to c. This can be interpreted as the function f(x) approaching L from both the sides of the c.
Let f(x) be a function that is defined on an open interval X containing x=a. (The value f(a) need not be defined.)
This definition is known as(ε, δ)-definitions or Cauchy definition for limit.
There (ε, δ)-definitions also the Heine definition of the limit of a function, which states that a function f(x) has a limit L at x=a, if for every sequence {xn}, which has a limit at a, the sequence f(xn) has a limit L. The Heine and Cauchy definitions of limit of a function are equivalent.
In formulas, a limit of a function is usually written as
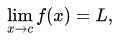and is read as "the limit of f of x as x approaches c equals L". The fact that a function f approaches the limit L as x approaches c is sometimes denoted by a right arrow, as in
|
English
