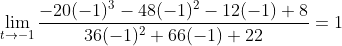Indeterminate Limits. Form 0/0
One of the most common indeterminate forms found in calculus is 0/0. It's called indeterminate because its value is uncertain and can vary from one limit to another. This particular expressions are obtained when attempting to find the limit of a rational expression. If both the numerator and the denominator of the function are zero, then the limit is indeterminate.
There are many techniques suitable to find indeterminate limits. The most-used and suitable for a great variety of problems is the L'Hopital's Rule (also known as L'Hospital Rule):
Application (single or repeated) of the rule usually converts an indeterminate form to an expression that can be easily evaluated by substitution. L'Hopital's rule states that under certain conditions, and being
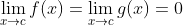
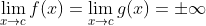

Example:
Find the value of the limit:
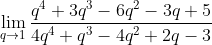
Substituting the value q=1 in the function we get
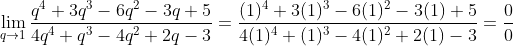
Applying L'Hopital's Rule:

Now this limit is determinate. Substituting q=1 again:
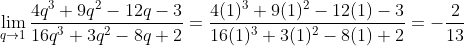
Example 2: Double Indeterminate
Some limits need more than one application of the L'Hopital's rule:
Find the value of the limit:
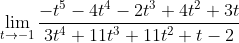
Substituting the value t=-1 in the function we get 0/0. Applying L'Hopital's Rule:
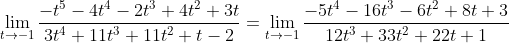
Substituting t=-1 produces another indeterminate expression 0/0. We need to apply for the second time:
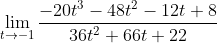
Now this limit is determinate. Substituting t=-1 for the last time: