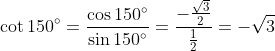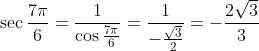Definition of Trigonometry
Is the branch of mathematics dealing with the relations of the sides and angles of triangles and with the relevant functions of any angles. There are six trigonometric functions of common use.
Coterminal Angles
Since there are 360 degrees (or 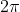 radians) in one rotation, an angle greater than 360 degrees
would indicate more than 1 full rotation. Shown on a circle, the resulting direction in which this angle’s
terminal side points would be the same as for another angle between 0 and 360 degrees.
These angles would be called coterminal
radians) in one rotation, an angle greater than 360 degrees
would indicate more than 1 full rotation. Shown on a circle, the resulting direction in which this angle’s
terminal side points would be the same as for another angle between 0 and 360 degrees.
These angles would be called coterminal
After completing their full rotation based on the given angle, two angles are coterminal if they terminate in the same position, so their terminal sides coincide (point in the same direction).
Example: Find the coterminal angle x in degress of the angle 750°, where 0 < x < 360°.
Since adding or subtracting a full rotation, (360 degrees), would result in an angle with
terminal side pointing in the same direction, we can find coterminal angles by adding or
subtracting 360 degrees. An angle of 750 degrees is coterminal with an angle of 750-360 = 390 degrees.
Since it's more than 360 degrees, we can find another coterminal angle of 390-360 = 30 degrees.
Example: Find the coterminal angle y in radians of the angle -195°, where 0 < y < 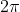 .
.
The angle is coterminal with -195° + 360° = 165°. Converting to radians and simplifying the fraction:
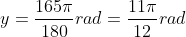
Example: Find the coterminal angle z in degrees of the angle
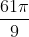 rad
where 0 < z < 360°.
rad
where 0 < z < 360°.
Converting to degrees:
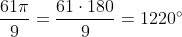
Subtracting again, the required angle is 500° - 360° = 140°
Example: Find the coterminal angle m in radians of the angle
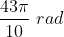 where 0 < m <
where 0 < m < 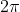 .
.
The angle is given and asked in radians, no conversion is needed. Every turn has 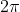 radians, thus we subtract
radians, thus we subtract
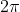 to the given angle as shown:
to the given angle as shown:
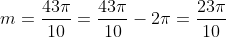
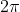 ,
so we subtract
,
so we subtract 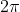 again:
again:
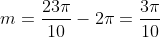
Sine and Cosine
For the point (x, y) on a circle of radius r at an angle of θ , we can define two important functions as the ratios of the sides of the corresponding triangle:
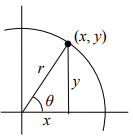
The Sine function is: 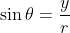
The Cosine function is: 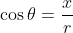
The Pythagorean Identity
For any angle θ:
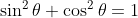
We can use this identity to find a cosine value of an angle if we know the sine value of that angle or vice versa. However, since the equation will yield two possible values, we will need to utilize the quadrant the angle lies in to help us find the desired value.
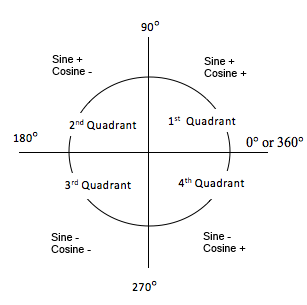
Example: Given 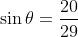 and θ lies in the second quadrant
and θ lies in the second quadrant 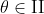 ,
find cos θ.
,
find cos θ.
We use the Pythagorean Identity to find the cosine:
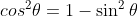
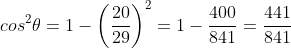
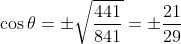
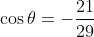
Special angles
There are some angles which are commonly encountered in problems and applications. Their sine and cosine values are easy to find and remember for use without the need of a computer, calculator or other physical or electronic means. The image below shows for each special angle the following ordered data: Angle measured in degrees, angle measured in radians, and an ordered pair with their cosine and sine respectively

Examples:
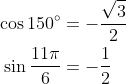
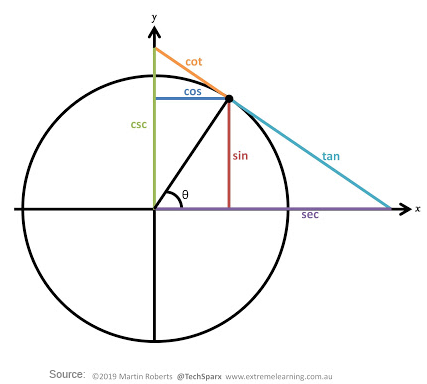
The Other Trigonometric Functions
In the previous section, we defined the sine and cosine functions as ratios of the sides of a right triangle in a circle. The triangle has 3 sides there are 6 possible combinations of ratios. While the sine and cosine are the two prominent ratios that can be formed, there are four others, and together they define the 6 trigonometric functions:
The Tangent: 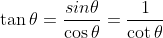
The Secant: 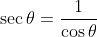
The Cotangent: 
The Cosecant: 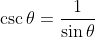
All these four trigonometric functions can be related back to the sine and/or cosine, thus finding their values for any angle is just a matter of substituting the known values of sine and cosine and simplify as required Examples: